本稿では、因果関係に関する2種類の数理的扱いについてまとめる。
・因果関係の強さを数理的に表現する
・数理的情報から因果関係を探索する
因果関係の大きさは、結果がどれだけ変わるか、で定義する
因果関係は、関係の有無だけではなく、どの程度の影響があるか、も重要である。
影響(効果)の大きさの測定方法としては、極めて直観的な、以下の定義が提案されている。
\( E(y_1-y_0) = E(y_1)-E(y_0) \)
これは、ある処置を行った場合\(y_1\)の期待値と、行わなかった場合\(y_0\)の期待値の差をもって影響の大きさとしようというものであり、ルービンの因果効果と呼ぶ。
もちろん、ある同じ個体に関して、処置を行った場合/行わなかった場合の両方の結果を得ることはできない。これは因果推論の根本問題と呼ばれる。
ランダムに構成された2つの集合に対して、一方だけに処置を行って結果を観察することになる。
ありものの調査データから測定することも必要
因果効果の測定にあたっては、ありもののデータを活用する方法も重要になる。
一例として以下のようなものがある。
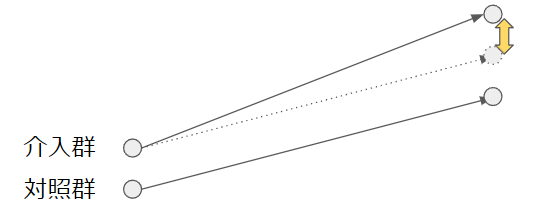
| 差の差分析 | 期間による自然変動が存在するとき | 自身の処置前後の変動幅と、同期間の対象群の変動幅を使って、処置部分だけの効果を推定する |
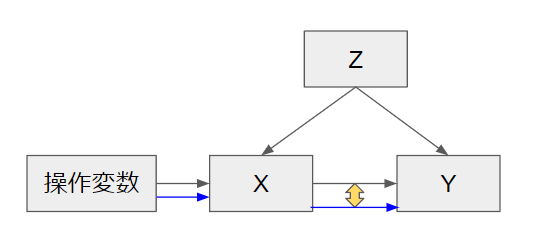
| 操作変数法 | 原因・結果の共通因子がある、かつ原因だけに直接影響を与える変数が存在するとき | 操作変数により原因の値だけが強制的に変わったときに結果がどれだけ変わるか、を測定する |
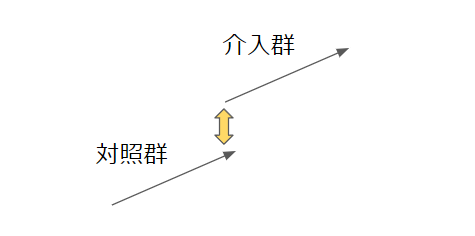
| 回帰不連続デザイン | 介入の有無を決める閾値があるとき | 閾値前後で結果がギャップアップしている幅を因果効果と推定する |
それぞれの手法を図解する。黄背景矢印が因果効果の大きさになる。
でもその前に、因果構造をデータから推測したい
因果効果の測定をするには、何が原因となって何に影響を与えているか、すなわち因果構造を事前に設定しておかないといけない。つまり、調べようとしている対象をよく知っていなければならない。
これはなんとかしたい。データはあるのだから、データを出発点にしてどういう因果関係になっているのかを逆に導き出したい。これが(統計的)因果探索という分野になる。
基本的なアイディアは以下のようになる。
・導出可能な構造はある程度限定する。具体的には、巡回的な構造を持っていないものとする。
・構造の中の1つの変数を固定したときに、他の変数同士は独立になるか共変性を持つか、によって取りうる構造を絞り込む。
構造次第で、必ずしも因果関係の特定までできるわけではない。
このあたり、因果探索はまさに発展中のジャンルと思しく、適用範囲の拡大が待たれるところである。
参考図書・Webサイト
1.滋賀大学が公開している因果探索入門の講義動画。全部で1時間強くらい。
因果推論・因果探索の両方にわたって、コンパクトでわかりやすい内容。


コメント